14 Markov Models

首先，我们要学习独立事件和条件独立。

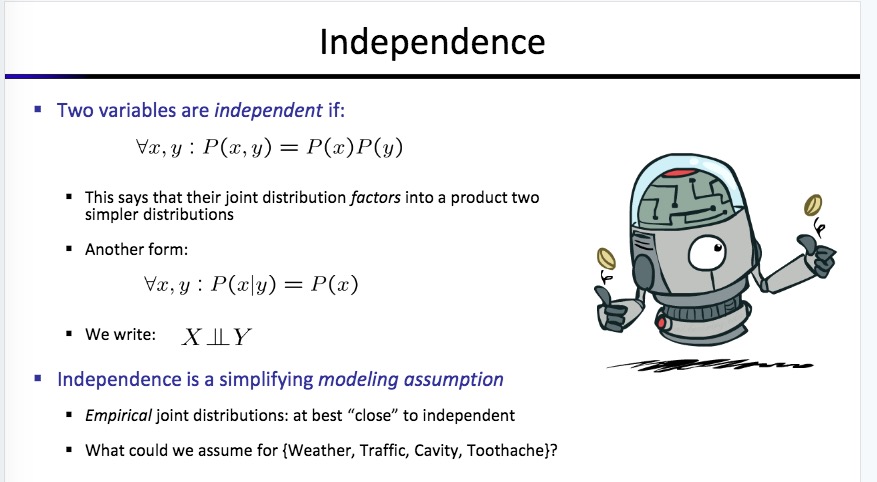
x事件和y事件独立 ： P(x,y) = P(x)*P(y)

x事件和y事件基于z事件独立 ： P(x,y|z) = P(x|z) * P(y|z)

然后这个东西会被应用到马科夫模型。

Markov model : 对于一串给定的状态，可以求出该段状态发生的概率

X1->X2->X3->X4->X5

P(X1) P(X2|X1) P(X3|X2) P(X4|X3) P(X5|X4)

马科夫模型：当前的时间Xt只与Xt-1有关，与X1.....Xt-2都无关

这样我们可以求出某一天发生某一事件的概率：

{sun, rain}

某一天为晴天的概率如下：

P(sun) = P(sun|rain)P(rain) + P(sun|sun)P(sun)

最后我们发现，当T足够长，P(sun)和P(rain)是趋于固定(Stationary Distribution)的。（即使头几天的值会和第一天的值有关联，但是第一天的影响在T足够大的时候可以被忽略，它只与CPT有关）

也就是回到最原始的Probability of sun and rain.

Independence

Conditional Independence

Probability Recap

Markov Models

Markov model : 对于一串给定的状态，可以求出该段状态发生的概率

X1->X2->X3->X4->X5

P(X1) P(X2|X1) P(X3|X2) P(X4|X3) P(X5|X4)

马科夫模型：当前的时间Xt只与Xt-1有关，与X1.....Xt-2都无关

Example of Markov Chain : Weather

基于马科夫模型，可以求出某一天发生某件事的概率，如下图所示：

Mini-Forward Algorithm

这是接着上一个例子，求出具体结果：

Stationary Distributions